Hyperhelices: A very plausible mechanism for hyper-dimensional torsion (a detailed long post)

[abellache]

Section 1: Fractals and their appearance in quantum phenomenon

Fractals are geometric shapes that exhibit self-similarity at different scales - that is, they contain smaller copies of themselves when you zoom in. Classic examples include the Koch snowflake, Sierpinski triangle, and Mandelbrot set. Unlike smooth curves or surfaces, fractals have fractional dimensions that fall between whole number topological dimensions. This fractal dimension quantifies how the complexity or detail of the shape changes as you examine it at finer scales.

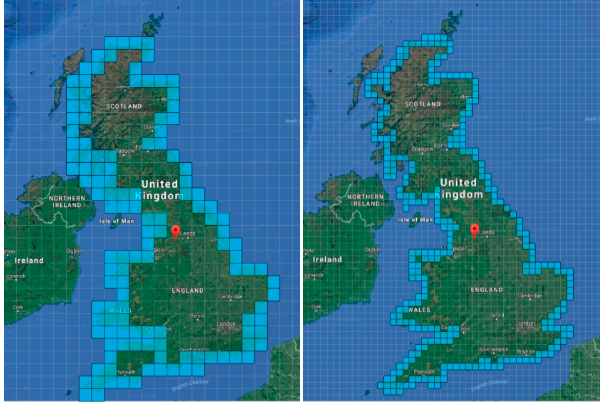
One common way to measure fractal dimension is the box-counting method. This involves covering the shape with progressively smaller boxes or grids and counting how many boxes are needed at each scale. For a smooth 1D curve, doubling the resolution (halving box size) would roughly double the number of boxes needed. But for a fractal curve, the number of boxes increases faster - if it increases by a factor of 3 when resolution doubles, that indicates a fractal dimension of about log(3)/log(2) ≈ 1.58. The coast of Britain famously has a fractal dimension of about 1.25.

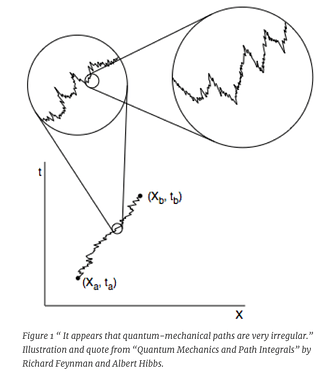
In the 1960s, Richard Feynman made the remarkable insight that the trajectories of quantum particles should be fractal curves with dimension 2. He reasoned that the Heisenberg uncertainty principle implies that measuring a particle’s position more precisely requires higher momentum uncertainty. This causes the velocity to fluctuate more wildly at smaller scales, producing an increasingly “jagged” path as you zoom in. Feynman showed mathematically that this effect would make quantum trajectories statistically similar to Brownian motion - the random walk of a particle buffeted by thermal collisions - which was already known to trace out fractal paths of dimension 2 in the limit of infinitesimal step size.

His main observations were:

1. Heisenberg’s uncertainty relation: How Heisenberg’s uncertainty principle relates position and momentum uncertainties. This relation is fundamental to understanding why quantum paths have fractal properties.

2. Feynman and Hibbs’ 1965 stated that “quantum-mechanical paths are very irregular” and that “the ‘mean’ square value of a velocity averaged over a short time interval is finite, but its value becomes larger as the interval becomes shorter.” This observation suggests non-differentiable, fractal-like behavior.

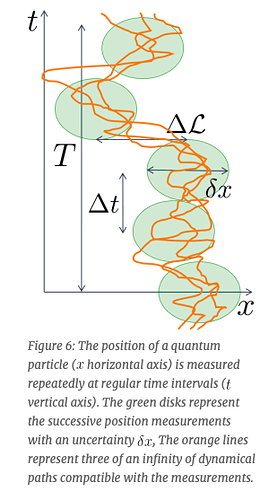
3. Mathematical derivation: The average distance traveled by a quantum particle scales with time as: <ΔX²> ~ Dt
   Where D is identified as an effective diffusion coefficient equal to ℏ/2m (ℏ is Planck’s constant, m is the particle’s mass).

4. Analogy with Brownian motion: The behavior of quantum paths resembles that of Brownian motion, which is known to have a fractal dimension of 2.

5. Scale-dependent velocity: As one look at shorter time intervals, the effective velocity of the quantum particle increases without bound, similar to how a fractal curve becomes increasingly “jagged” at smaller scales.

6. Transition in fractal dimension: There appears to be a transition in the fractal dimension of the path depending on the resolution scale. At very fine scales (below the de Broglie wavelength), the path behaves with D=2, while at larger scales it transitions to classical behavior with D=1.

[abellache]

Section 2: Why Fractal space requires hyperdimensional mathematics

This fractal property emerges from the fundamental principles of quantum mechanics, particularly the Heisenberg uncertainty principle. As we try to pinpoint a particle’s position more precisely, we inevitably introduce greater uncertainty in its momentum, leading to more erratic motion at finer scales. This scale-dependent behavior is a hallmark of fractal geometry, where zooming in reveals ever-increasing complexity.

The fractal dimension of 2 for quantum paths has profound implications. It suggests that quantum particles, in some sense, fill space more completely than classical particles. While a classical trajectory is a simple line with dimension 1, a quantum trajectory is a tangled, space-filling curve. This property helps explain phenomena like quantum tunneling, where particles appear to pass through energy barriers, and the wave-like behavior of matter in quantum mechanics. It’s as if the particle, through its fractal trajectory, “explores” all possible paths simultaneously, leading to the probabilistic nature of quantum mechanics.

The concept of fractal spacetime introduces a fundamental shift in how we view the fabric of reality. In this framework, space and time are not smooth and continuous at all scales, but rather exhibit a fractal structure at very small scales. This fractal nature has profound implications for the mathematical description of physical phenomena, particularly in quantum mechanics.

One of the most significant consequences of fractal spacetime is the necessary introduction of complex numbers into the least action principle. In classical physics, the principle of least action states that the path a system takes between two points is the one that minimizes the action. However, in a fractal spacetime, the very concept of a “path” becomes more intricate. The fractal nature of space means that as we look at smaller and smaller scales, paths become increasingly convoluted and unpredictable. To account for this behavior, we need to introduce a complex-valued action. This complex action allows us to describe the multitude of possible paths a particle might take in a fractal spacetime, capturing the inherent uncertainty and “fuzziness” of quantum phenomena.

From this complex-valued least action principle, it becomes possible to derive a generalized form of the Schrödinger equation. This derivation is remarkable because it shows how quantum mechanics, traditionally viewed as a fundamental theory, can emerge from purely geometric considerations of fractal spacetime. The wave function in this context is not just a mathematical tool, but a direct representation of the fractal nature of spacetime itself. The imaginary part of the complex action gives rise to the phase of the wave function, while the real part corresponds to its amplitude.

Perhaps one of the most intriguing aspects of this approach is how it naturally leads to a hydrodynamic description of quantum mechanics. In this picture, the wave function can be interpreted as describing a fluid-like substance permeating all of space. The real part of the Schrödinger equation corresponds to a continuity equation for this fluid, ensuring conservation of probability, while the imaginary part can be interpreted as a quantum version of the Euler equation in fluid dynamics.

Quantum interference, for instance, can be visualized as the interaction of waves in this quantum fluid. The bizarre behavior of quantum particles, such as their ability to seemingly be in multiple places at once, can be understood as properties of waves in the quantum fluid. Moreover, this approach offers new ways to think about quantum entanglement and non-locality, potentially as features of the global structure of this quantum fluid. By recasting quantum mechanics in the language of fluid dynamics, we gain new insights and potentially new mathematical tools for tackling some of the most perplexing aspects of quantum theory.

[abellache]

Section 3: Hyperhelices and torsion in quantum hyper dimensional spacetime.

This is the section I want to arrive at, but before I had to make sure the background is clear.

Hyperhelices are the entire point I wanted to arrive at in this entire post and represent a geometric concept that bridges the gap between classical and quantum descriptions of nature. First introduced by N.H. Fletcher in 2004, a hyperhelix is a structure that consists of a rod coiled into a helix, which is then coiled into another helix, and so on, potentially through an infinite number of orders. This recursive helical structure provides a classical analogue for some of the most puzzling aspects of quantum mechanics, particularly the concept of spin and hidden dimensions.

To understand hyperhelices, let’s start with a simple helix, which we can call a hyperhelix of order 1. Now imagine this helix itself being coiled into a much larger helix - this would be a hyperhelix of order 2. This process can be continued indefinitely, creating hyperhelices of higher and higher orders. Each level of coiling introduces a new dimension of complexity to the structure. Importantly, the behavior of waves propagating along a hyperhelix depends on the scale at which you observe it. At the largest scale, it might appear as a simple straight line, but as you zoom in, you reveal more and more of its intricate helical structure.

The concept of hyperhelices can be understood in terms of torsion in a hyperdimensional space. Torsion, in geometric terms, is a twisting of space around a line. In the context of hyperhelices, each level of helical structure can be thought of as introducing torsion in a new dimension. For a hyperhelix of order N, we can imagine it as existing in an N+1 dimensional space, where each additional dimension corresponds to the torsion introduced by a new level of helical structure. This hyperdimensional perspective provides a geometric interpretation for the “hidden dimensions” often discussed in some theories of quantum mechanics and string theory.

One of the most intriguing aspects of hyperhelices is how they naturally give rise to a concept analogous to quantum spin. In quantum mechanics, spin is an intrinsic angular momentum of particles that has no classical counterpart. However, the behavior of waves propagating along a hyperhelix mimics some key features of quantum spin. As waves travel along the hyperhelix, they acquire a phase that depends on the helical structure. This phase accumulation is similar to how the wavefunction of a spinning quantum particle evolves. Moreover, the discrete nature of the helical orders in a hyperhelix corresponds to the quantized nature of spin in quantum mechanics.

The emergence of spin-like behavior from the geometry of hyperhelices provides a compelling classical analogue for this quantum phenomenon. It suggests that the seemingly mysterious quantum property of spin might be understood geometrically as a consequence of the structure of space itself at very small scales. Hyperhelices demonstrate how complex quantum behaviors can emerge from relatively simple geometric principles.

[abellache]

Section 4: As below so above, hyperhelixes in biology.

The principle of torsion, central to the hyperhelix concept, is also fundamental in biological structures. DNA, perhaps the most famous helical structure in biology, exhibits multiple levels of coiling and supercoiling, each introducing torsion at a different scale. This multi-scale torsion in DNA is not just a structural feature but is intimately linked to its function, influencing processes like transcription and replication. Similarly, the cytoskeleton, composed of structures like microtubules and actin filaments, often displays helical or twisted conformations that introduce torsion at the cellular level. This torsion plays a role in cell mechanics, division, and intracellular transport.

The scaling principles observed in hyperhelices might help explain how biological structures achieve remarkable efficiency and functionality across different scales. For instance, the fractal-like branching of neurons or the vascular system allows for efficient space-filling and material transport, much like how the nested structure of a hyperhelix efficiently “fills” its space at different scales. The concept of critical points in scale transitions, as seen in hyperhelices, might correspond to critical points in biological systems where quantum effects become relevant, potentially explaining some of the more puzzling aspects of biological efficiency and information processing.

Moreover, the emergence of spin-like properties in hyperhelices offers an intriguing perspective on the role of chirality in biology. Many biological molecules, exhibit a preferred handedness or chirality. This fundamental asymmetry, crucial for life as we know it, might be understood as a manifestation of underlying geometric principles similar to those that give rise to spin-like behavior in hyperhelices. The interplay between structure and function in biology, often involving complex rotations and torsions across multiple scales, resonates with the way complex behaviors emerge from the geometric structure of hyperhelices.

[abellache]

Thanks for your patience in reading through all of this feel free to provide any criticizms. I still haven’t finished the SS brotherhood of the bell and will later do the philosopher stone and will order Unified Field theory book. So if you have any pointers or ideas that come to mind related to these books, please share.

Refrerences and bibliography

Maybe of interest to @vardas3 @omnimatter and other fellow Gizars with a technical background

Helicalised fractals

On the arithmetic of fractal dimension using hyperhelices

Fractal dimension of quantum paths

Hyperhelices: A classical analog for strings and hidden dimensions

Wave propagation on helices and hyperhelices: a fractal regression

The Pauli equation in scale relativity

Relativity in resolution-scale space

Possible symmetry (E8 Lie group) that the “philosopher’s stone” could have. Based on the idea for fractal symmetry:

Quantum criticality in an Ising chain: experimental evidence for emergent E8...

[abellache]

NB: I found this funny music on Youtube titled “hyper-helices” for the music savvy amongst you I wonder what to do you think?

hyper-helices (Symphony, pt 2)

[psilocybeaustralis]

My first thought on the diagrams - the bottom right reminded me of those “spiders” on Mars pictures I find your posts on science/physics etc fascinating - please continue !!