After finishing the philosopher stone and giving the original Giza death star (volume 2 plus the revisited version) a look I want to write-up what directions has the reading of those books lead me to. While Einstein’s general relativity provides an elegant description of gravity in terms of curved spacetime, many experiments mentioned in these books plus in the SS brotherhood of the bell suggest that picture may be incomplete.
Two concepts that have gained significant attention in theoretical physics are torsion and fractal spacetime. These ideas, while distinct, both aim to extend our understanding of spacetime beyond the smooth, curved manifold of general relativity.
Torsion, in the context of gravity, refers to a twist in the fabric of spacetime. Mathematically, it’s represented by the antisymmetric part of the affine connection, a geometric object that describes how vectors change as they’re moved through spacetime. While Einstein’s theory assumes this connection is symmetric (torsion-free), more general theories allow for non-zero torsion.
Torsion can be crudely understood and having a space in which parallelograms dont close. The torsion tensor T measures the deviation from that closure.
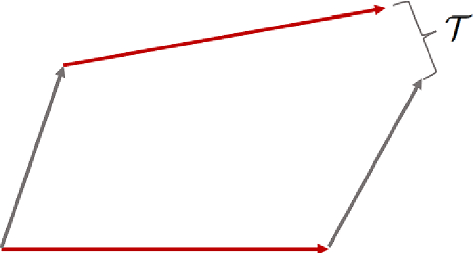
The inclusion of torsion in gravitational theories isn’t merely a mathematical exercise. It opens up new possibilities for understanding the universe. For instance, torsion naturally couples to the intrinsic angular momentum (spin) of particles, providing a geometric description of spin in curved spacetime.
This spin-torsion coupling leads to some intriguing consequences. In some theories, it gives rise to a nonlinear generalization of the Dirac equation - the fundamental equation describing the behavior of spin-1/2 particles like electrons. This nonlinearity manifests as a universal spin-spin interaction, hinting at a geometric origin for some of the fundamental forces in nature.
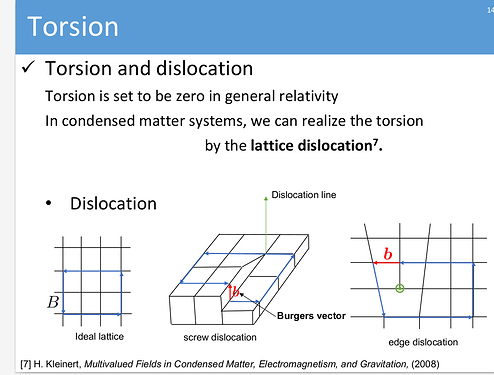
But the influence of torsion extends far beyond the realm of fundamental particles. In condensed matter physics, torsion emerges as a powerful tool for describing the behavior of electrons in crystalline materials with defects. Crystal dislocations - lines of disrupted atomic order - can be elegantly described using the language of torsion.
Recent work has shown how torsion, manifested through screw dislocations in a crystal, can induce chiral currents reminiscent of those seen in the presence of magnetic fields. This “torsional magnetic effect” bridges the gap between the abstract geometry of spacetime and the tangible world of materials.
The connection between torsion and materials doesn’t stop at static defects. In the burgeoning field of topological materials, particularly Weyl and Dirac semimetals, torsion plays a crucial role. These exotic materials host low-energy excitations that behave like relativistic particles, making them ideal playgrounds for exploring the interplay between quantum mechanics, relativity, and geometry.
As we zoom out from individual particles and crystals to consider the collective behavior of quantum fields, torsion continues to exert its influence. The emerging field of quantum field hydrodynamics - which describes the flow-like behavior of quantum fields - provides a fascinating arena for studying torsion effects.
Recent theoretical work has shown how torsion modifies the hydrodynamic description of chiral fluids - collections of particles with a preferred handedness. Torsion introduces new terms in the constitutive relations that govern the behavior of these fluids, leading to novel transport phenomena.
While torsion provides a way to enrich the geometric structure of spacetime, another approach suggests a more radical departure from our usual understanding of spacetime. This is the concept of fractal spacetime, most notably developed in the theory of scale relativity.
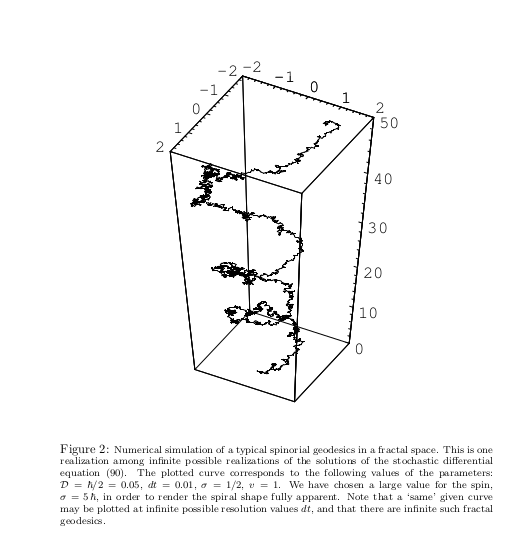
In scale relativity, spacetime is not just curved, but fractal and non-differentiable at quantum scales. This fractal structure is proposed as the origin of quantum behavior, with quantum mechanics emerging as the mechanics of fractal spacetime.
One of the most intriguing aspects of scale relativity is its treatment of spin. In this framework, spin is not an additional postulate but a natural consequence of the fractal geometry of spacetime. It arises from the complex, multi-scale nature of a particle’s trajectory in fractal spacetime.
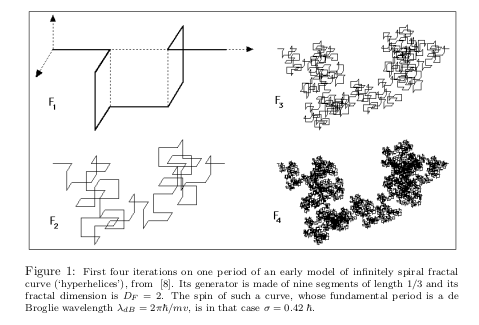
The fractal nature of spacetime in this theory leads to a two-valuedness of velocity, which is key to deriving quantum mechanical equations. This two-valuedness, when extended to three dimensions, naturally leads to a quaternionic structure that gives rise to the Pauli matrices and spin.
Both torsion and fractal spacetime approaches provide geometric interpretations of spin, suggesting a deep connection between the structure of spacetime and the intrinsic angular momentum of particles. This convergence hints at a fundamental link between these seemingly disparate concepts.
However, the fractal nature of spacetime at small scales poses challenges to our usual geometric concepts. For instance, the notion of parallel transport, fundamental to our understanding of curvature and torsion, becomes problematic in a fractal spacetime where smooth, continuous paths may not exist.
This observation leads to a reality with multiple layers: perhaps our current geometric descriptions, including those incorporating torsion, are approximations of a more complex underlying “source”. Just as fluid dynamics emerges from the collective behavior of molecules, perhaps our smooth spacetime emerges from the ‘flow’ of more fundamental entities. This idea resonates with approaches in quantum gravity and offers potential new avenues for unifying gravity with other forces.
In this picture, torsion might represent an intermediate level of description between the possibly fractal or hydrodynamic nature of spacetime at the smallest scales and the smooth spacetime of general relativity.
In this hierarchical view of spacetime, we might envision three levels of description:
- At the largest scales, the smooth, torsion-free spacetime of general relativity
- At intermediate scales, a geometry incorporating torsion
- At the smallest scales, a fractal, possibly hydrodynamic description
This perspective suggests that torsion could emerge as an effective description of the underlying fractal structure when viewed at certain scales. It would capture some of the departures from smooth geometry without fully describing the fractal nature of spacetime at the smallest scales.
Conclusion: the concepts of torsion and fractal spacetime represent “the esoteric” frontier in solving the enigma of the alchemist texts. From an experimental perspective, while directly probing the fractal nature of spacetime or detecting torsion remains challenging, their effects in condensed matter systems offer promising avenues for indirect tests. Precise measurements of transport properties in topological materials could reveal signatures of torsion-induced phenomena, providing tabletop probes of exotic spacetime geometry…
I find it intriguing that The Urantia book, as well, supports a continuing-creation theory. I hope you Brainiacs can help us figure out what is REALLY going on!! 