Quantum mechanics and relativity are completely derivable from fractal geometry + the ether

Science and Technology
#1

I’ve come across many such derivations but scale relativity theory is the most mathematically convincing. Basically if you assume that at smaller scales geodesic paths are continuous but non differentiable as any bubble chamber experiment would show then you automatically derive that spacetime is fractal

You can then derive the uncertainty principle:

And even the shrodinger equation

All you need is: general relativity + fractal spacetime. Adapting the calculus is complicated but apparently not impossible.

#2

A unfied field theory would then become far more accessible. The theory is still young but it rederives the wave-particle duality, entanglement, and is geometric. Things that bohmian mechanics could not do.
To me physics should be about how things emerge from the medium, as hermetic philosohy teaches.

Wonder what you guys think of this approach.

#3

By “fractal space-time” here, I’m assuming we are dealing with Dan Winter – correct?

1 Like
#4

I dont know who he is. I will search for him.
I was thinking about Laurent Nottale.

The textbook is super technical. But he does re-derives most known results and the randomnes of quantum mechanics becomes simply uncertainty over the derivative of fractal functions. That uncertainty can be modeled as an imaginary stochastic term added to the traditional derivative. Similar to brownian motion but with an i.

That is enough to re-derive shrodinger equation, and and the uncertainty relation, plus a field theory. The sacrifice is that calculs becomes more difficult because of all the stochastic terms in complex space.

#5

You’re always going to find difficulty in defining space and time as a cross or dot product hence “space-time” as a single manifold. Each is it’s own independent manifold with features that cannot be attributed to any universal relationship, with exception of Energy (E). It is in the topological level of the fractal embedding procedure, right at the definitions of manifold and continuum, that the fundamental inadequacy of the method arises with respect to its object. The manifold is taken to be merely a mapping surface - not the map, its surface and its depth, which consists of a wave energy field composed of two commensurate, mutually imbricated but distinct manifolds.

I cannot get into his work in detail at the moment, but there are several positives from a surface level:

  1. The author understands the non-equivalence of mass and charge;
  2. He (presumably) lists Leibniz as author of the Calculus (really rare) and I’ll bet you this man had terrible difficulty publishing;
  3. Space (as such) is “inhomogenous” or in other words anisotropic;

All good things distinguishing the work from the mainstream.

#6

Ok but are these different manifolds coupled in the filed equations? Its kind of important.

#7

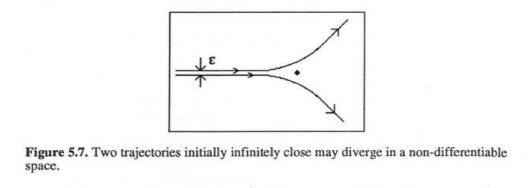
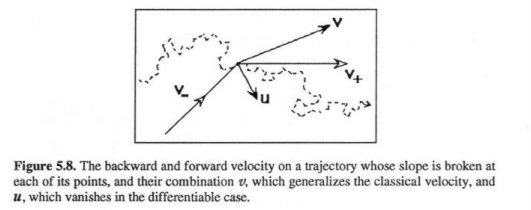
Yes, let’s take an example of why space-time is incommensurate.

In Newtonian theory (what Notalle calls classical mechanics), events take place in absolute Space, and that Space is Euclidean in three dimensions. Three lengths of spatial coordinates can identify any event per this system theory -

S=x^3

Whereas the set T of temporal moments of an event, ie, the location of the event in Time, is only the one-dimensional timeline (t1), such that the structure A of Space and Time is simply the Cartesian or cross product of Space and one-dimensional Time -

So for a given classical system, we have …

A = ST = x^3 *t^1

Flattened continua (space-time) take recourse to Minkowsky space-time, which differs from Newtonian Space AND Time in that is not defined by the Cartesian product S x T = x3 * t1, but by a pseudo-Euclidean, flattened Space in four dimensions -

Therefore, in Relativity (and hence Notalle) we have …

S=x^4

In Special Relativity, one encounters a continuum defined as four-dimensional, additive space-time in the function for the square power of the latter that permits its expression in terms of the c2 constant we find in the Einstein field famous E=mc^2 -

So, for Relativity and anything else building upon it …

dS2 = dx1^2 + dx2^2 +dx3^2 - c^2 (dt^2)

Since we must follow the Einstein prescription for “c” as a unity function and write the timeline strictly as the length, t=x4, which corresponds to our Minkowski-Einstein postulate, we have -

dS^2 = dx1^2 + dx2^2 +dx3^2 - dx4^2

Pay cautious attention to what just happened in the final term as it becomes evident how timeline (dx4^2) is now a negative term in four-dimensional Space.

More importantly, it is apparent that such a ‘projected’ continuum could never describe an energy continuum or the superimposition of manifolds that form distinct energy multiplicities. The objection raised here and expounded upon by many physic dissidents, most notably for me, Harold Aspden, and du Gabriel (see Fermat’s Last Theorem and Einstein’s Four Light Postulates for details, is the use of ADDITION to couple the dimensions. As you point out, this is a critical step and the central issue in coupling continuum elements, field or otherwise.

We object not simply to the abuse of the sign of addition to a couple of dimensions—primarily when volume itself defines Euclidean.
Space is l3, and it makes explicit the powers of multiplication implicit in the exponent. The totality of the mathematical operations undergirds the reduction of a continuum S to x^4 that must be apprehended and rejected as fiction. If you go through the vid chats released shortly after Dr. Farrell published “The Demon in the Eukr,” I presented a brief commentary on the paper Levi-Civita published addressing the use of tensors in mapping these flat geometries.

It is not energy that is a function of Space and Time, but the latter two manifolds, which are a function of energy, from which they also derive their intrinsic commensurability - an insight completely unknown to present-day physics. That is, neither space and time nor space-time are vessels in which energy is held. Energy, as such, is the progenitor of both Space and Time and all commensurate activities known as multiplicities, waveforms, and their superimpositions, resulting in particulate matter.

Flattened continuum geometries are merely content with representing the multiplicity of Time as if it were just a special (and single) dimension of the multiplicity Space as shown above. This is the case for both classical mechanics, Relativity, and Quantum car mechanics.

But consider the classical dimensional function for energy - it is written as a function of three distinct dimensionalities (mass m, length l, time t), deemed to be irreducible, and in a product relationship -

E = m l^2 t^-2

Precisely because such an abstract form of energy affects ponderability (as it carries the property we denote as mass), one may properly speak here of mechanical energy and its effects. But what to say of massfree energy, imponderable energy - what is the natural form of its function?

E = l^3 t^-2

E=(not mc^2) but E=ST=l^3t^2

The versor equilavlent:

E=ST

Energy is a function of space and time, not space-time; energy is not within the vessel of space-time; space and time are energetic features.

In this way, we find it apparent how energy is a function of a given volume of Space, and its cross-product superpositions with Time become resonant synchronicities. This provides for both Space and Time to be defined energetically.

1 Like
#8

I should add here that this system of understanding was developed by A. MacFarlane, extended and confirmed by Charles Proteus Steinmetz, and then completed by Eric. P. Dollard. The use of the term manifold is from Rene Thom. And, this is totally reconcilable with the topological notation used by Dr. Farrell in his description of the TMM, as well as transcendental interpretations of a personal deity.

Macfarlane:

Steinmetz, Charles P.

Dollard, Eric P

https://versoralgebra.com/

1 Like
#9

Thanks for the references. I will look as I need to see more precisely how can such manifolds bé defined.

#10

I also hear a lot inaccurate propositions about relativity, such as it precludes the existence of the ether. Nothing can be further from the truth. Relativity is more like an epistemic break from the need to build a physics from an absolute frame of reference. You can actually introduce the ether if you want, its just impossible to measure its speed. Which makes the theory unpractical unless you get back to relative predictions. Its very well explained here:

#11

Like Einstein, the math is beyond me. However, if I understand your physics, zero point energy is real and possible to access. If so, you may have laid the groundwork leading to unlimited energy.

1 Like
#12

I always refer back to Ken Wheeler…

1 Like
#13

It means it’s real but it’s impossible to see. Barring some clever way to poke a glitch in the architecture of the cosmos.

In the scale relativity treatment its starts with modeling the medium/ether as a Madelung fluid, then introducing hydrodynamics, curvature, and torsion. This means one does not have to give up neither relativity nor quantum theory. Just introduce scale transformations that keep the equation invariant. Its an addition to Lorentz transformation, adding scaling symmetries basically.

#14

For those that are not repelled by excessive technical detail:

They even have a free version I think its a preprint version of the book:

#15

The passages where one can derive a fluid dynamics equation purely by applying principles of calculus on fractal spaces are

Capture d’écran 2024-08-31 à 23.38.18

And:

Capture d’écran 2024-08-31 à 23.36.14
Capture d’écran 2024-08-31 à 23.36.14492×596 82.3 KB

Simply put, just expressing a simple geodesic equation in a fractal spacetime creates a diffusion equation with dissipation and dispersion terms. You get a wave inside a hydrodynamic fluid expression, AND you have the complex numbers which Shrodinger introduced without explaining why, as he himself did not understand why it worked.

#16

To conclude about how all this relates to the topological principle I will quote one of the paper on this framework:

Thus, we come up with a physical model of the world matter per se, the matter free of space: a fluid with no interaction, only inertially described, just the fluid necessary for SRT. For once, this is not a physical structure, but only a physical model, because the matter does not allow for penetration of the space within it. And only if we have matter penetrated by space can we say that we are dealing with a physical structure, otherwise not. Therefore, one of the sections of the present work will be dedicated to the explanation of the inertia and its mathematical extension. The explanation will be done on purely geometrical grounds, whereby the holographic principle - a natural principle, we should say, for the matter in bulk - is brought to bear at the level of a surface, where the surface is this time physical: the surface of separation of matter from space. The physical definition of such a surface is by fragments, representing portions of matter just about to enter the reality of a physical structure. This plainly gives physical sense to holographic principle in its most general undertaking.

In other words, the holographic principle is a pure expression of the topological metaphor. And maybe the key to understanding the physics of the zero-point or the ether.

#17

Thanks for the explanation — I think. Let me try to clarity my understanding of your terms of analysis.

When you refer to torsion, I think you are suggesting twisting of either the ether or is it space time?

Are suggesting that Einstein’s theory of relativity is incorrect in that there is no space time but space and time are separate?

When you speak of fluid dynamics do you mean that you are treating the ether (or space time) as a fluid for your mathematical analysis?

When you mention scalar invariability are you stating that the effect which you are propounding does not vary with size? In other words the properties remain the same no matter the physical dimension — whether on a quantum scale or our physical universe scale?

When you answered that zero point energy is real but inaccessible without poking a hole in the fabric of the universe, were you referring to the ether, space time or another dimension or parallel universe?

Thanks for taking the time to educate me as to the meaning and signifcance of your article on our lives.

1 Like
#18

When people give you a figure for the speed of light that’s the two way speed. i.e the time it takes light to hit and object and bounce back to the sender. We then divide twice the distance by that time. In doing so we assume isotropy. That light has the same speed in every direction. In fact no one has ever measured the one way speed of light. It turns out you can’t. Its hidden from us. So that’s the limitation that says Michelson and Morley did not disprove the ether.

But that’s a problem in that if we can’t tell how fast light travels at every direction we dont know what direction the ether actually flows.

The existence of this fundamental indetermination means we have an epistemological limit to what we can know. Almost like we live in a holographic reality and absent some way to see past the hologram, we are stuck with relative points of view at best.

#19

We hit a similar epistemic barrier when trying to observe phenomenon that are very small. The medium is highly jittery and turbulent at those small scales and thus can’t be apprehended in a statistically robust way at larger, much smoother scales.

This is also true for larger scales (galaxies etc) when observing how their behavior emerges from smaller objects

The fundamental problem is in loss of information as trajectories become irregular and it becomes impossible to have reversibility
Capture d’écran 2024-09-01 à 12.27.27

Even the notion of velocity at the neighborhood of a given point is not well determined. One has to talk for a given point x about the slope of f before x and another slope after x. Thus giving two velocities, the before and after.

Capture d’écran 2024-09-01 à 12.27.57

Cartan had already found a way around this problem by introducing complex numbers in the notion of derivatives. And this is the true origin of complex numbers in quantum mechanics.

Capture d’écran 2024-09-01 à 12.26.26
Capture d’écran 2024-09-01 à 12.26.26513×632 50.5 KB

#20

About Torsion. That is very complicated to understand without the topological metaphor. Indeed, rather than assuming that spacetime is curved. Cartan suggested to Einstein to split the problem into a euclidean incorporal space and the medium in which matter and the ticking of time emerges.

However, with Madelung fluid, one can go even further and remove the notion of curvature altogether and replace it with torsion as a consequence of the variation of density of the medium (or Madelung fluid in our case). This is of course conceptually problematic as the space in which we represent the medium and its density is not corporal. It is assumed that the space in question is just a tool, an interface we use because we cannot probe what the deeper reality is.

Capture d’écran 2024-09-01 à 12.44.30
Capture d’écran 2024-09-01 à 12.44.30685×577 50.3 KB

The math for this new vision essentially build on top of the Madelung transform and its connection between hydrodynamics and the Shrodinger equation

Capture d’écran 2024-09-01 à 12.59.21